|
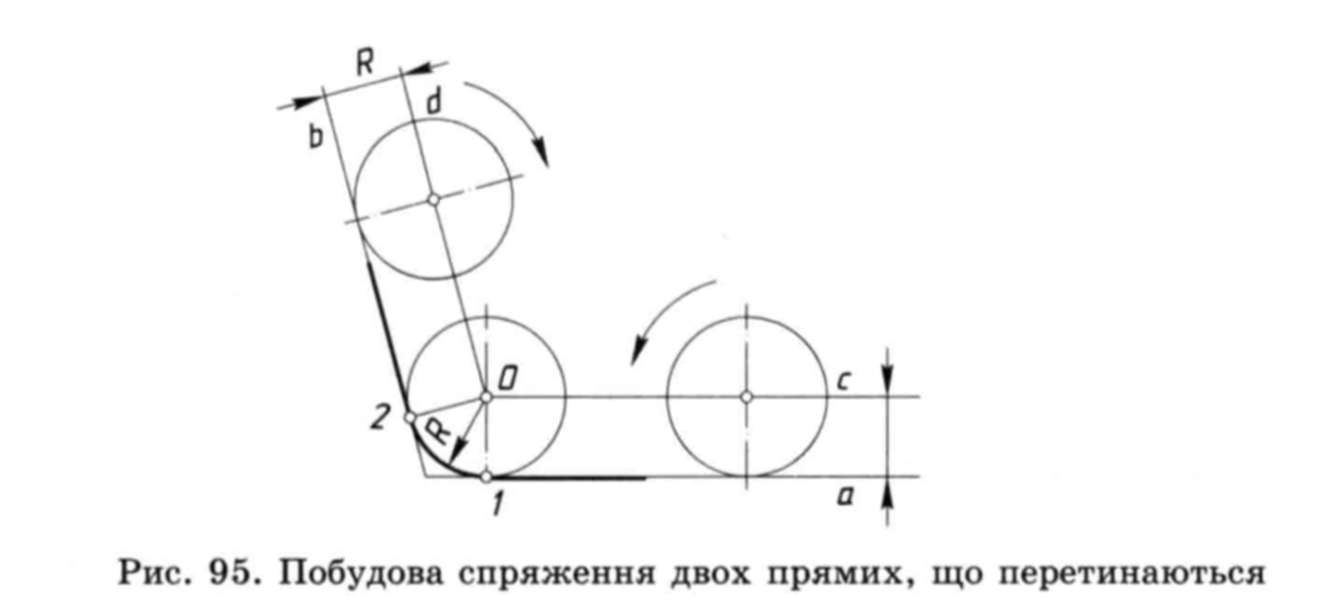
Спряження двох прямих, що перетинаються. Дві прямі, що перетинаються, можуть утворювати прямий, гострий і тупий кути. Для всіх трьох випадків спосіб побудови один і той же. Він полягає ось у чому. Дуга плавного переходу від однієї прямої до іншої має радіус R. Якщо це дуга кола, то для її проведення слід знати положення центра цього кола. Нехай таке коло «закотилося» в кут між двома прямими (рис. 95). Це коло може «закотитися» вздовж прямої а. Тоді його центр О опише свою траєкторію у вигляді прямої с і на незмінній відстані від прямої а — ця відстань весь час дорівнює радіусу R. Так само, якщо «закочувати» коло вздовж прямої b, то його центр опише траєкторію у вигляді прямої d і на відстані від неї, що також дорівнює радіусу R.
«Закочене» в кут коло одночасно доторкається до обох прямих (а і Ь), і його дуга утворює плавний перехід між цими прямими. Центр кола тепер знаходиться на перетині прямих cid, тобто точка перетину прямих cid являє собою центр спряження. Особливістю прямих с і d є їх паралельність заданим прямим на відстані радіуса спряження R від них.
Згадайте, що дотична до кола і радіус, проведений у точку дотику, завжди взаємно перпендикулярні (див. рис. 94, а). Тому, щоб побудувати точки спряження прямих а і Ь дугою радіуса R, слід опустити перпендикуляри з точки О на задані прямі. Одержані точки 1 і 2 (рис. 95) будуть точками спряження, через які і повинна бути проведена дуга спряження радіуса R.
Отже, побудову спряження двох прямих, що перетинаються, дугою заданого радіуса R (рис. 96, l) виконують у такій послідовності:
1. Паралельно першій із спряжуваних прямих проводять допоміжну пряму на відстані радіуса спряження R від неї (рис. 96, ll).
2. Паралельно другій із спряжуваних прямих проводять другу допоміжну пряму, також на відстані радіуса спряження
|
|